• Home
  • Article
  • Perbandingan De Novo Programming dan Linear Programming

Perbandingan De Novo Programming dan Linear Programming

10 Oct 2017

  1. 1.              Metode De Novo Programming

    Menurut Tobacanon dalam Iriani (2012:18) suatu cara untuk melihat sistem dimana selain mengoptimalkan sistem yang telah ada, juga menyarankan perancangan suatu sistem yang optimal. Yang dititik beratkan pada membuat suatu desain yang optimal terhadap sistem yang ada dengan produktivitas tinggi yang memiliki beberapa kriteria.

Menurut Sarjono (2015:57-58), pendekatan metode De Novo Programming dalam menyelesaikan masalah optimasi dilakukan dengan pendekatan system secara total, yang berarti bahwa selain menentukan kombinasi output yang terbaik, juga dapat memberikan saran penggunaan sumber daya dengan berdasarkan pada anggaran yang ada. Dalam metode De Novo Programming kendala sumber daya atau bahan baku diatur seefisien mungkin sehingga tidak menghasilkan sisa.

Formulasi De Novo Programming tidak hanya berkaitan dengan menentukan campuran output terbaik, tetapi juga dengan campuran masukan terbaik juga.

Menurut Tabucanon dalam Iriani (2012 : 21) apabila dalam formulasi model De Novo Programming tidak ada kendala–kendala yang lain, hanya terdiri dari satu fungsi tujuan dan satu kendala (kendala keterbatasan anggaran), maka penyelesaiannya dengan langkah–langkah sebagai berikut :

  1. Cari Max j (Cj / vj)

Perbandingan (Cj / vj) menggambarkan keuntungan dari produk j (bila fungsi tujuan adalah memaksimumkan profit) atau nilai tujuan biaya per unit yang tercapai dari kombinasi sumber – sumber yang digunakan untuk memproduksi produk j. Tujuan dari langkah ini adalah untuk mencari produk mana yang paling menguntungkan untuk diproduksi.

  1. Untuk Max (Cj / vj) yang diperoleh, katakanlah (Ck / vk) yang berhubungan dengan variabel Xk, maka jumlah dari Xk yang harus diproduksi adalah Xk = B / vj, dan Xkmerupakan jumlah produk yang paling optimal yang harus diproduksi.

Dimana :

vj= variabel cost untuk membuat i unit produk j (j = 1, 2, 3, ……., n)

C j= koefisien biaya yang terdapat pada semua fungsi tujuan

Hal ini menunjukkan bahwa sumber–sumber yang dimiliki akan digunakan untuk memproduksi produk Xk sebagai produk yang paling menguntungkan dengan jumlah yang sesuai dengan anggaran (budget), apabila tidak ada kendala – kendala lain.

Apabila terdapat jumlah permintaan yang terbatas pada setiap produk, maka formulasi De Novo Programming dapat diselesaikan dengan langkah-langkah sebagai berikut :

  1. Cari Max j (Cj / vj)

Untuk Max j (Cj / vj) katakanlah sebagai contoh (Ck / vk) untuk produksi Xksedemikian rupa sehingga tidak melampui batas dari permintaan atau batas maksimum yang dianggarkan (budget).

  1. Jika anggaran tidak digunakan sepenuhnya pada saat memproduksi X k, maka cari produk lain yang menguntungkan, selanjutnya dengan menggunakan Max j (Cj / vj), dimana j ≠ k.
  2. Kembali ke langkah (2) sampai anggaran yang ada sudah digunakan sepenuhnya.

Dari langkah-langkah di atas dapat dibuat suatu diagram alir sebagai berikut :

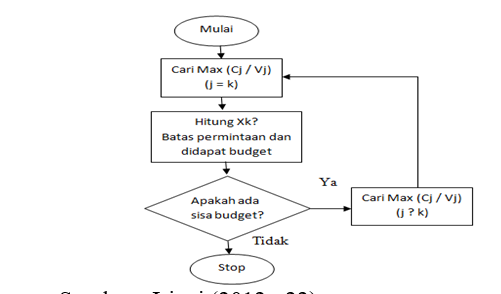
Sumber : Iriani (2012 : 22)

 

2.              Metode Linear Programming

Menurut Subagyo (2007:122), Linear programming (LP) adalah cara untuk menyelesaikan persoalan pengalokasian sumber-sumber terbatas di antara beberapa aktivitas bersaing, dengan cara terbaik yang mungkin dilakukan. Menurut Murugan (2013:184), pemrograman linier adalah sebagai model matematis yang terkait dengan masalah optimasi bentuk standar, baik untuk memaksimalkan atau meminimalkan fungsi tujuan yang berkaitan dengan kendala spesifik.

Menurut Heizer & Render, (2017:739) linear programming mempunyai empat sifat umum diantaranya:

  • Permasalahan LP bertujuan untuk memaksimalkan atau meminimalkan beberapa kuantitas (biasanya keuntungan atau biaya). Sifat ini dapat kita simpulkan sebagai fungsi tujuan dari masalah LP. Tujuan utama dari sebuah perusahaan pada umumnya adalah untuk memaksimalkan keuntungan jangka panjang. Pada kasus lainnya seperti dalam kasus distribusi truk/angkutan atau sistem maskapai penerbangan, tujuan biasanya untuk meminimalkan biaya pengiriman.
  • Adanya batasan atau  kendala, yang membatasi sejauh mana tujuan yang ada dapat tercapai. Misalnya, mengambil keputusan untuk memproduksi berapa banyak unit masing-masing produk di lini produk perusahaan, dibatasi oleh tenaga kerja dan mesin yang tersedia. Oleh karena itu, untuk memaksimalkan atau meminimalkan kuantitas (tujuan dan fungsi) bergantung pada sumber daya yang terbatas (kendala).
  • Harus ada beberapa program alternatif tindakan untuk dipilih misalnya, jika sebuah perusahaan memproduksi tiga produk yang berbeda, manajemen dapat menggunakan LP untuk memutuskan bagaimana cara mengalokasikan sumber daya produksi yang terbatas (tenaga kerja, mesin, dan sebagainya). Jika tidak ada alternatif yang dapat dipilih, maka LP tidak diperlukan.
  • Tujuan dan batasan dalam permasalahan LP harus dinyatakan dalam hubungan dengan pertidaksamaan atau persamaan linear.

 

Model pemrograman linear mempunyai tiga unsur utama yaitu :

  1. Variabel keputusan

Variabel keputusan adalah variabel persoalan yang akan mempengaruhi nilai tujuan yang hendak dicapai. Didalam proses permodelan, penemuan variabel keputusan tersebut harus dilakukan terlebih dahulu sebelum merumuskan fungsi tujuan dan kendala-kendalanya. (Siswanto, 2007:25)

  1. Fungsi Tujuan

Menurut Mesra B (2016:7), fungsi adalah hubungan matematis antara suatu variabel dengan variabel lainnya. Unsur-unsur pembentuk fungsi adalah variabel,koefisien dan konstanta. Menurut Rahmi dan Suryani (2007:26), tujuan yang hendak dicapai harus diwujudkan ke dalam sebuah fungsi matematika linear. Selanjutnya, fungsi itu dimaksimumkan atau diminimumkan terhadap kendala-kendala yang ada.

  1. Fungsi Kendala

Menurut Rahmi dan Suryani (2007:26), manajemen menghadapi berbagai kendala untuk mewujudkan tujuan-tujuannya. Kenyataan tentang eksistensi kendala-kendala tersebut akan selalu ada. Kendala dengan demikian dapat diumpamakan sebagai suatu pembatas terhadap kumpulan keputusan yang mungkin dibuat dan harus dituangkan ke dalam fungsi matematika linear. Dalam hal ini, sesuai dengan dalil-dalil matematika, ada tiga macam kendala yaitu : Kendala berupa pembatas, Kendala berupa syarat, Kendala berupa keharusan.

 

Perbedaan Metode Linear Programming dan Metode De Novo Programming

No Linear Programming De Novo Programming
1 Asumsi bahwa sumber daya terbatas pada jumlah yang telah ditetapkan sebelumnya. Asumsi bahwa sumber daya menjadi terbatas karena adanya jumlah maksimum dari budget (anggaran)
2 Analisa sumber telah di tentukan dan sumber tidak dapat dikendalikan perolehannya, karena bahan baku yang di miliki harus dibeli sesuai dengan ukuran minimum yang telah ditentukan sebelumnya. Analisa dilakukan sebelum sumber daya yang dimiliki di beli, sehingga sumber daya belum dapat ditetapkan dan sumber daya yang ada dapat dikendalikan dan diperoleh sesuai dengan anggaran yang telah ditetapkan.
3 Tidak sensitif terhadap faktor harga dari sumber daya, dan pemberian harga terjadi selama analisa sensitivitas Sensitif terhadap faktor harga. Sumber daya telah diberi harga berdasarkan penetapan harga aktual.
4 Tidak selalu memiliki kendala keterbatasan budget (anggaran) Faktor keterbatasan budget (anggaran) merupakan elemen penting karena hal ini dijadikan ukuran dari sumber daya yang dibutuhkan.
Pada beberapa kasus masih terdapatnya sisa pengunaan sumber daya. Solusi dari model atau pendekatan ini adalah dengan utilitas sumber daya yang penuh tanpa adanya sisa.
Haryadi Sarjono